Como fazer uma análise de correlação em dados de séries temporais com o R
Essa é uma tradução. o texto original (em inglês) pode ser encontrado aqui
O que é análise de correlação cruzada?
O conceito de correlação é o mesmo usado em dados que não são de séries temporais: identificar e quantificar a relação entre duas variáveis quantitativas. Devido à natureza contínua e cronologicamente ordenada dos dados das séries temporais, é provável que haja algum grau de correlação entre as observações das séries.
Medir e analisar a correlação entre duas variáveis, no contexto da análise de séries temporais, pode ser entendido por dois angulos diferentes:
Analisar a correlação entre uma série e seus lags, pois alguns dos lags anteriores podem conter informações preditivas, que podem ser utilizadas para prever eventos da série. Os métodos mais populares para medir o nível de correlação entre uma série e suas defasagens são a função de autocorrelação (FAC) e a função de autocorrelação parcial (FACP).
Analisar a correlação entre duas séries para identificar fatores exógenos ou preditores, que possam explicar a variação da série ao longo do tempo. Nesse caso, a medição da correlação é normalmente feita com a função de correlação cruzada.
Olhar para essas características pode ser muito útil para encontrar novos recursos para usar na etapa de modelagem, também para entender padrões de comportamento ao longo do tempo.
Como realizar análise de correlação em dados de séries temporais usando R?
Encontrar uma maneira de fazer isso no R pode ser complicado, devido à grande quantidade de pacotes, e cada pacote usa um tipo diferente de objeto. O objetivo deste artigo é orientá-lo por três maneiras diferentes de fazer a análise de correlação, sendo a última uma maneira geral (organizada).
Um breve aviso antes de começar, este artigo não pretende explicar toda a teoria por trás da análise de correlação e para uma explicação mais completa, você pode acessar esta ótima referência: Forecasting: Principles and Pratice. O livro está disponível de graça aqui https://otexts.com/fpp3/
As Diferentes Abordagens
Vamos configurar nosso ambiente:
# packages for this tutorial
# first approach
library(feasts)
library(tsibble)
library(lubridate)
# second approach
library(TSstudio)
library(plotly)
# third approach
library(tidyverse)
library(timetk)
library(lubridate)Banco de Dados
Usaremos um conjunto de dados do Stack Overflow, que contém o número de perguntas para cada mês de 2009 a 2019, em diferentes tópicos. Você pode acessar os dados neste link.
O conjunto de dados contém 9 recursos diferentes em relação às palavras-chave usadas nas perguntas do Stack Overflow, mas aqui usaremos apenas as colunas r e python.
library(readr)
dados_StackOverflow = read_csv("~/Documentos/GitHub/Base_de_dados/MLTollsStackOverflow.csv")
# selecting columns to use in this tutorial
stackoverflow_tbl <- dados_StackOverflow %>%
select(month, r, python)
head(stackoverflow_tbl)# A tibble: 6 × 3
month r python
<chr> <dbl> <dbl>
1 09-Jan 8 631
2 09-Feb 9 633
3 09-Mar 4 766
4 09-Apr 12 768
5 09-May 2 1003
6 09-Jun 5 1046Farei uma transformação básica no conjunto de dados que deve nos ajudar durante o tutorial e em todos os métodos.
# convert to date
stackoverflow_prep_tbl <- stackoverflow_tbl %>%
mutate(date = str_glue("20{month}"),
date = yearmonth(date) %>% as_date()) %>%
select(date, r, python, -month)# A tibble: 132 × 3
date r python
<date> <dbl> <dbl>
1 2009-01-01 8 631
2 2009-02-01 9 633
3 2009-03-01 4 766
4 2009-04-01 12 768
5 2009-05-01 2 1003
6 2009-06-01 5 1046
7 2009-07-01 51 1165
8 2009-08-01 47 1143
9 2009-09-01 139 1169
10 2009-10-01 73 1424
# … with 122 more rowsPrimeira abordagem
O primeiro método que será mostrado usa o objeto ts, um formato embutido no R para séries temporais. Com o objeto ts temos uma boa integração com o pacote TSstudio e boas funções interativas para usar.
# ts function is responsible to convert to ts object
stackOverflow_ts <- ts(data = stackoverflow_prep_tbl[, c("python", "r")], # selecting 2 variables
start = c(2009, 01), # start date
end = c(2019, 12), # end date
frequency = 12)Agora podemos ver todas as informações sobre a série temporal que foi criada com a função ts.
ts_info(stackOverflow_ts) The stackOverflow_ts series is a mts object with 2 variables and 132 observations
Frequency: 12
Start time: 2009 1
End time: 2019 12 Com este resumo, é possível ver que temos duas variáveis, que representam duas séries temporais diferentes. Cada série temporal representa uma linguagem (R e python).
ts_plot(stackOverflow_ts,
title = "Perguntas mensais no Stack Overflow",
Ytitle = "# Questions",
Xtitle = "Year")Com este gráfico, vemos que o python tem uma tendência mais acentuada do que o R em relação ao número de perguntas feitas no Stack Overflow. A série temporal não possui um padrão sazonal, mas é possível ver um componente ciclico em ambas as séries temporais.
Vejamos os gráficos de correlação!
Análise de Defasagens I
O pacote TSstudio não possui nenhuma função para plotar as medidas FAC e FACP, e para isso utilizamos as funções internas acf e pacf. A desvantagem aqui, para mim, é que o objeto gerado por essas funções não é um objeto ggplot2 e perdemos todos os belos recursos da gramática dos gráficos.
Obviamente, você pode passar pelos dados e tentar plotar no ggplot2 sozinho, mas será um pouco trabalhoso.
Para séries temporais da linguagem R:
par(mfrow = c(1, 2))
# acf R time series
stackOverflow_ts[, c("r")] %>%
acf(lag.max = 300,
main = "Autocorrelação - R")
# pacf R time series
stackOverflow_ts[, c("r")] %>%
pacf(lag.max = 300,
main = "Autocorrelação Parcial - R")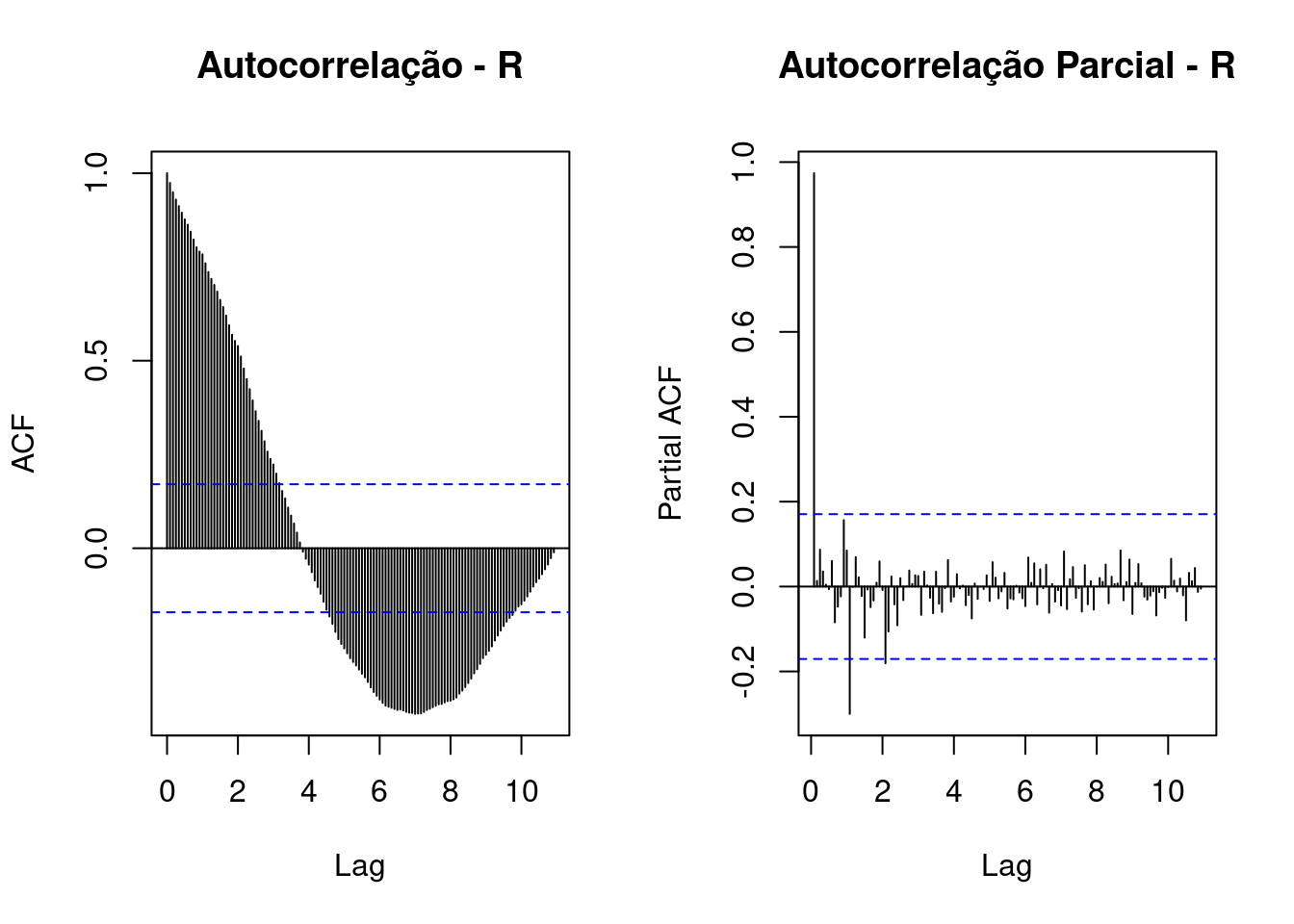
Para séries temporais da linguagem Python:
# acf Python time series
stackOverflow_ts[, c("python")] %>%
acf(lag.max = 300,
main = "Autocorrelação - Python")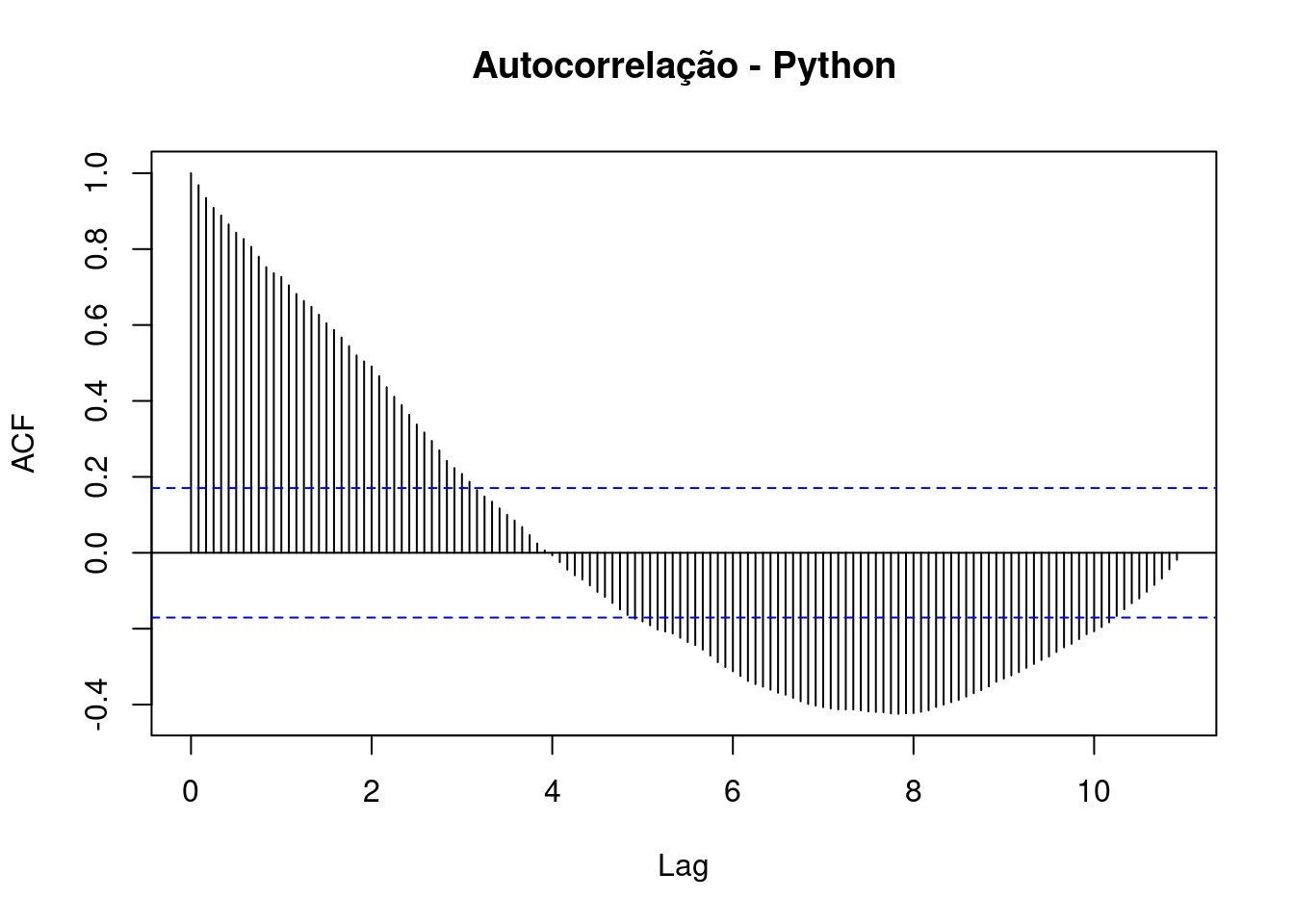
# pacf Python time series
stackOverflow_ts[, c("python")] %>%
pacf(lag.max = 300,
main = "Autocorrelação Parcial - Python")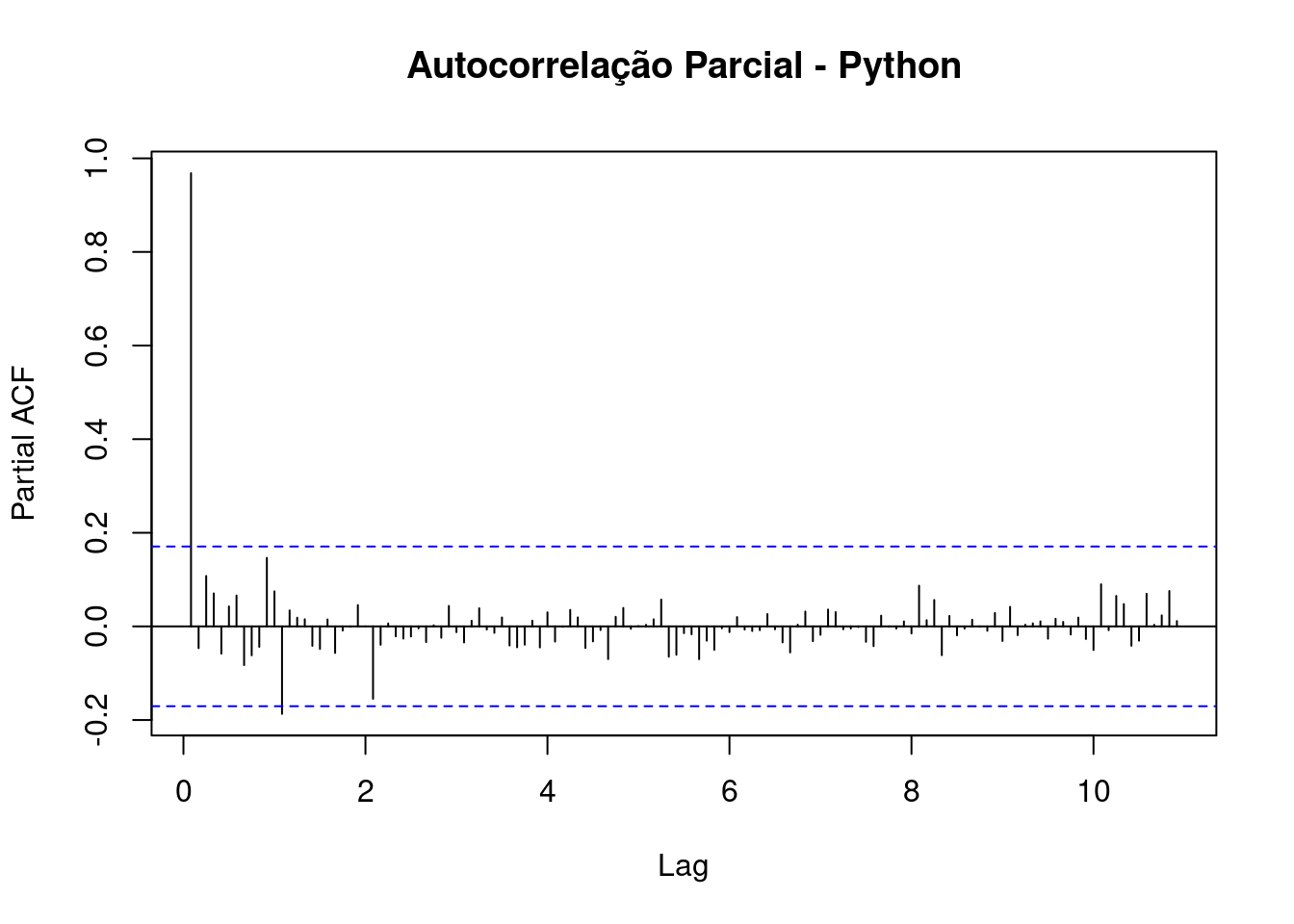
Em todos os gráficos, temos características que precisam ser explicadas:
linhas azuis: Essas linhas referem-se a um intervalo de significância, as barras que passam por essas linhas têm significância estatística.
eixo y: pontuações de correlação.
eixo x: Aqui temos a indicação dos lags. Cada defasagem corresponde a 12 meses, ou seja, quase 11 defasagens.Observe que, observando os gráficos FAC, tanto para as séries temporais do R quanto do Python, temos uma correlação maior com os atrasos mais recentes, que são perdidos com o tempo. Com defasagens mais distantes é possível perceber que temos uma correlação negativa com dados recentes.
A Autocorrelação Parcial é um pouco diferente, essa correlação “parcial” entre duas variáveis é a quantidade de correlação entre elas que não é explicada por suas correlações mútuas com um conjunto especificado de outras variáveis.
Por exemplo, se estamos regredindo uma variável Y em outras variáveis X1, X2 e X3, a correlação parcial entre Y e X3 é a quantidade de correlação entre Y e X3 que não é explicada por suas correlações comuns com X1 e X2.
Resumindo, quando olhamos para o gráfico FACP, queremos saber cada lag que tenha informações relevantes para usar como preditor em uma previsão futura. Quanto maior o escore do FACP, melhor.
E, em nossos gráficos, vemos que ambas as séries temporais têm um lag (mais próximo do lag 1) que pode ser útil.
Não basta apenas saber qual pontuação de correlação tem a pontuação mais alta, é importante ver visualmente como esses pontos são distribuídos. Nisso, o TSstudio possui uma ótima função interativa, chamada ts_lags.
# Looking at lag plots
ts_lags(stackOverflow_ts,
lags = c(2, 20, 30, 40, 50, 80)) %>% # choosing what lags to plot
layout(title = "Series vs Lags")Warning in ts_lags(stackOverflow_ts, lags = c(2, 20, 30, 40, 50, 80)): The
'ts.obj' has multiple columns, only the first column will be plotAnálise de causalidade I
Somente olhar para o padrão passado de uma série nem sempre é uma boa ideia. A principal armadilha desse método é que ele falhará sempre que as mudanças nas séries derivarem dos fatores exógenos. O objetivo da análise de causalidade, no contexto da análise de séries temporais, é identificar se existe uma relação de causalidade entre as séries que desejamos prever outros potenciais fatores exógenos.
Tenha cuidado com o fato de que correlação não implica causalidade, apenas procuramos algo que possa ajudar o modelo de previsão. Em nosso caso atual, podemos apenas ver se existe algum atraso nas séries temporais do R correlacionadas às séries temporais do Python.
# ccf time series
par(mfrow=c(1,1))
ccf(stackOverflow_ts[, c("r")], stackOverflow_ts[, c("python")],
lag.max = 300,
main = "Cros-Correlation Plot",
ylab = "Cross-Correlation-Function - CCF")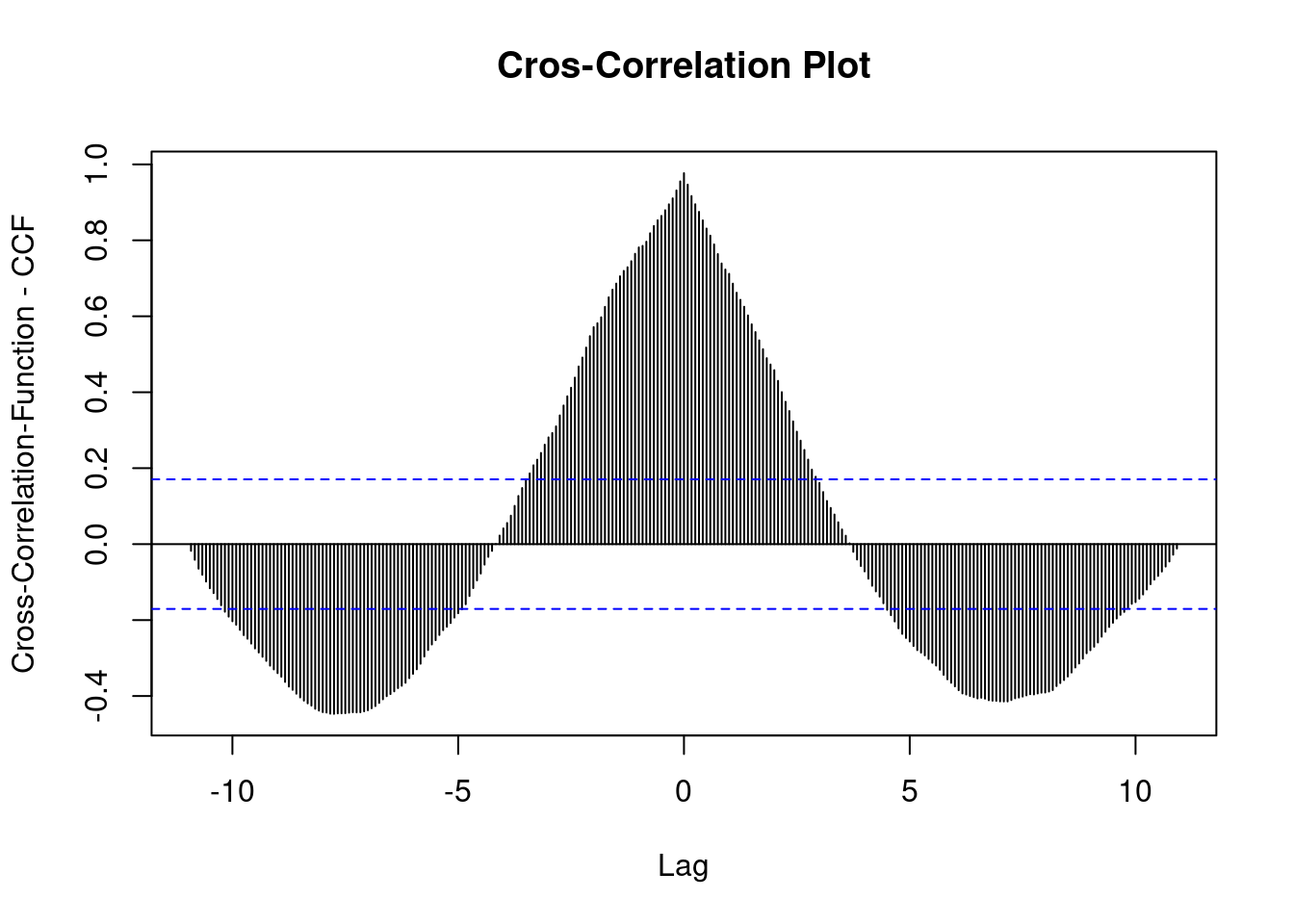
Vemos que a pontuação mais alta está nas defasagens recentes, e algumas pontuações entre 5 e 10 têm uma relação negativa.
O gráfico está nos dizendo que atualmente (na data do conjunto de dados) o crescimento das questões do R está altamente correlacionado com as questões do Python.
Segunda abordagem
Essa segunda abordagem usa um objeto que é chamado de tsibble, como um tibble com um índice de datas implícito. Então, vamos converter nosso tibble em um tsibble.
stackoverflow_prep_tsbl <- stackoverflow_prep_tbl %>%
mutate(date = yearmonth(date)) %>%
pivot_longer(cols = c(r, python), names_to = "names", values_to = "value") %>%
as_tsibble(key = names,index = date) # specifying the time series in the objectDiferentemente do que fizemos antes, aqui os dados foram convertidos de wide para um formato longitudinal (long), melhor para os gráficos.
Olhando para o objeto criado, vemos a indicação de um intervalo dessas observações [1M] (mensal). E também vemos a variável chave, que é uma forma de indicar quantas séries temporais existem neste objeto. É possível ter diferentes combinações de feições para fazer uma nova série temporal no objeto.
Com os objetos prontos, podemos agora realizar a análise de correlação por esta segunda abordagem. Tente que a interpretação gráfica já foi feita, e aqui vou apenas explicar a diferença entre os métodos.
Análise de Defasagem II
Ao contrário do TSstudio, não temos plots de interatividade, todos os plots são estáticos, mas são objetos do ggplot2 e nos permitem utilizar os conceitos da gramática de gráficos.
Um problema com essas funções é que elas podem se comportar de maneira diferente do esperado. Conectando os dados às funções FAC (acf) e FACP (pacf), podemos ver automaticamente os gráficos facetados entre todas as séries temporais dentro do objeto. Mas se tentarmos simplesmente visualizar a série ao longo do tempo, não será possível facetar. Não é um grande problema, e você pode plotar usando o ggplot normalmente (veja o código).
# looking at the data
stackoverflow_prep_tsbl %>%
feasts::autoplot()Plot variable not specified, automatically selected `.vars = value`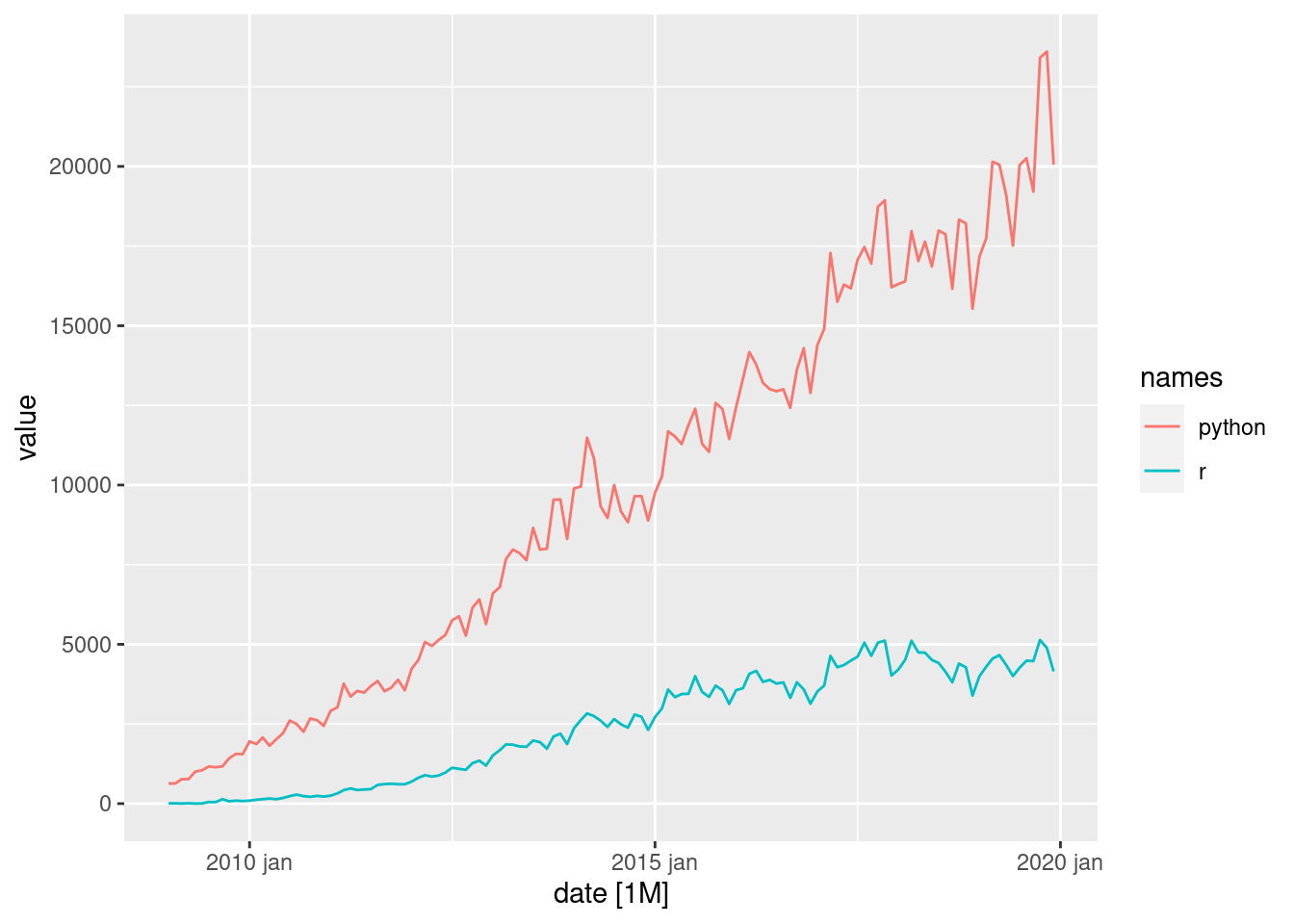
# looking at the data facet way
stackoverflow_prep_tsbl %>%
ggplot(aes(x = date,
y = value,
color = names)) +
geom_line() +
facet_wrap(~names, scales = "free_y")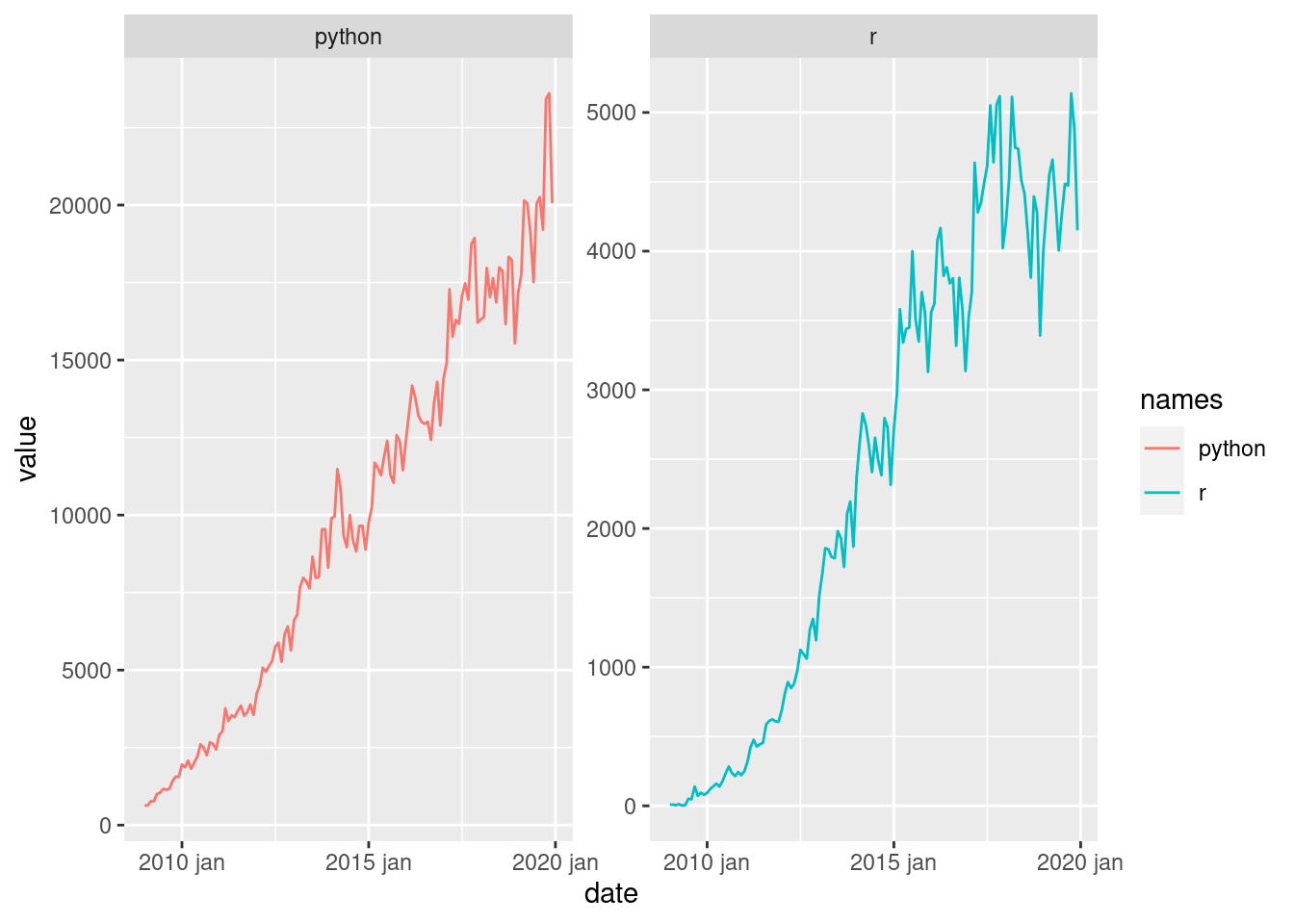
# lag plots
stackoverflow_prep_tsbl %>%
filter(names == "python") %>%
gg_lag(value, geom="point")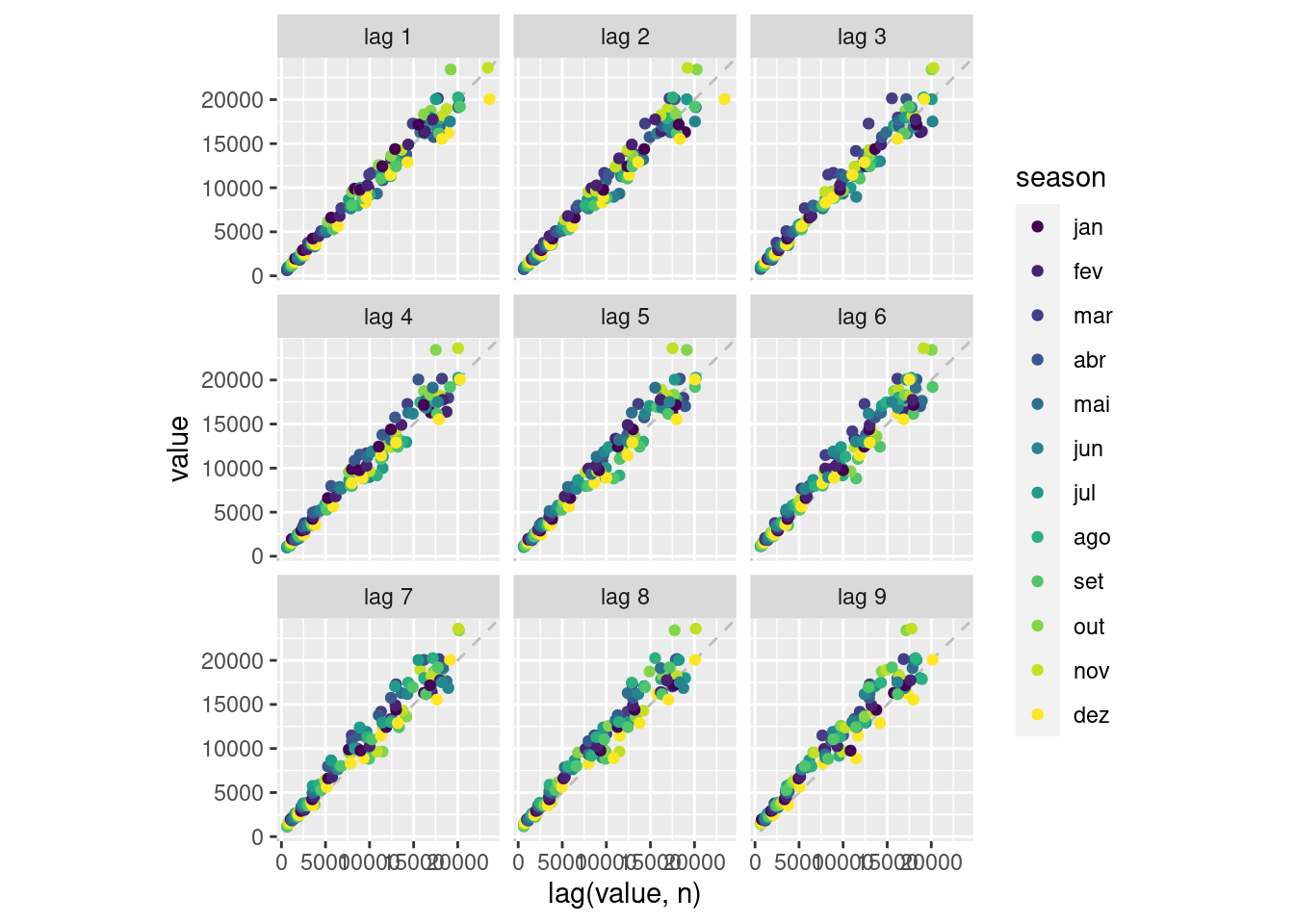
# acf
stackoverflow_prep_tsbl %>%
ACF(value, lag_max = 300) %>%
autoplot()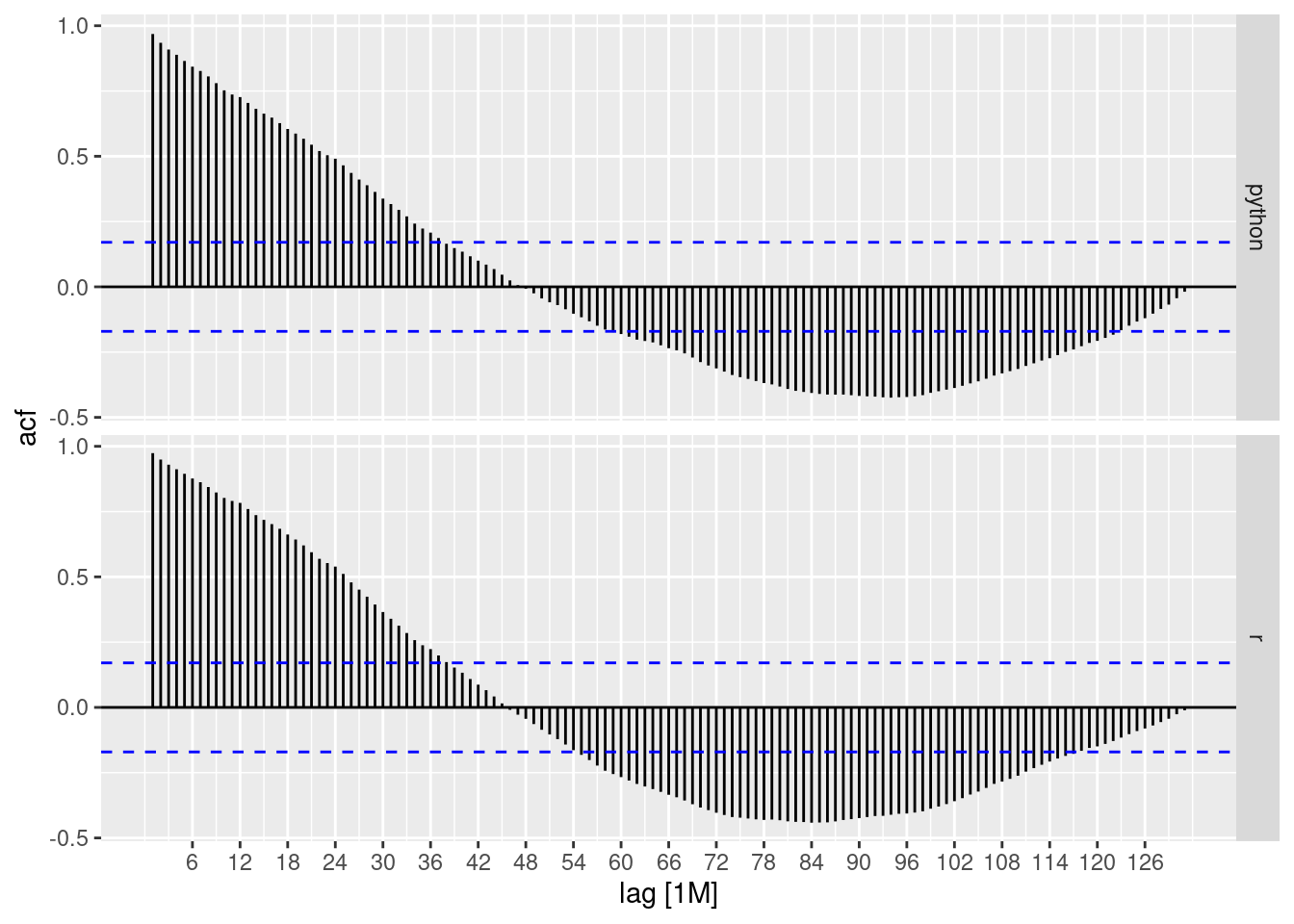
# pacf
stackoverflow_prep_tsbl %>%
PACF(value, lag_max = 300) %>%
autoplot()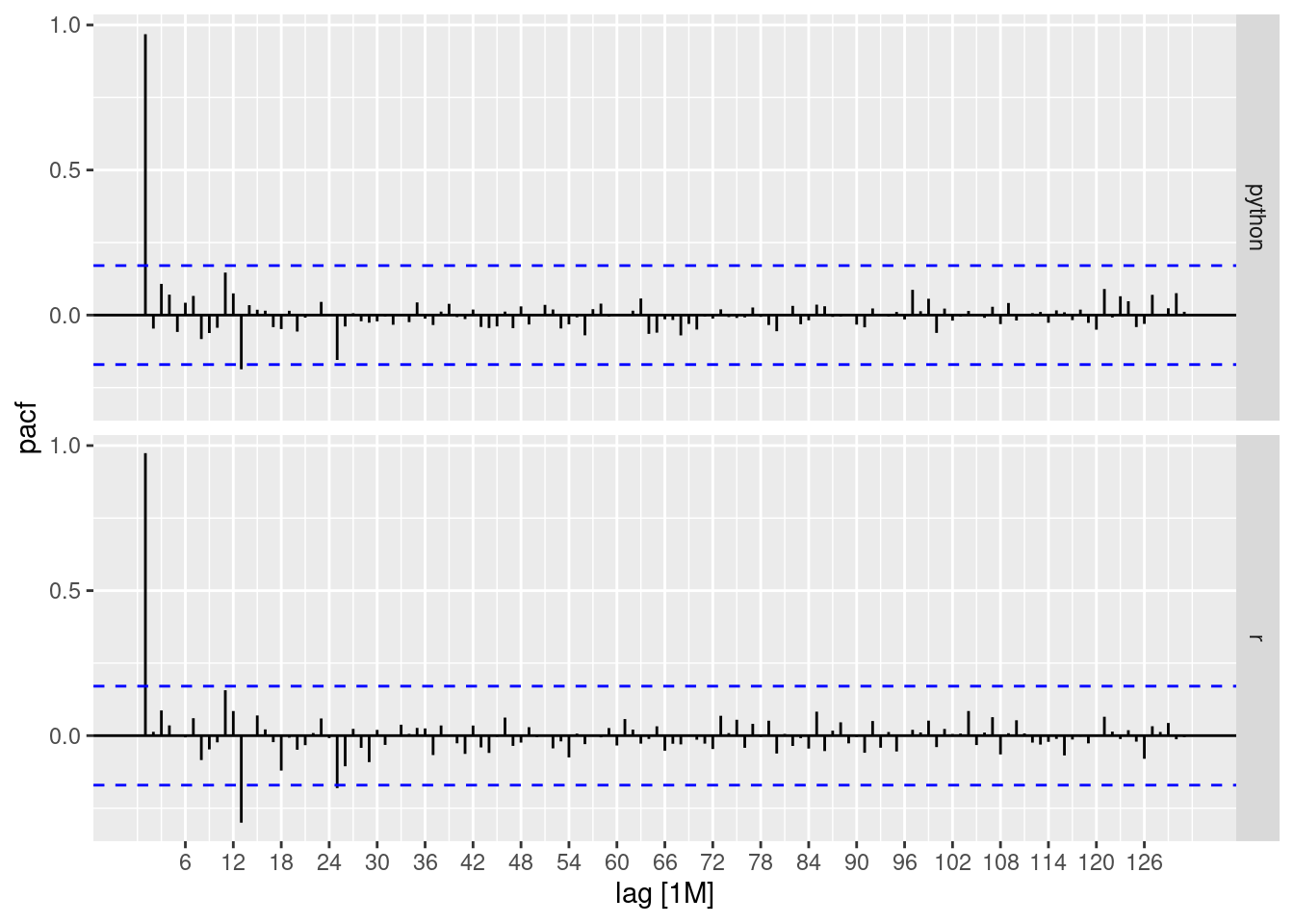
Análise de causalidade II
# ccf
stackoverflow_prep_tsbl %>%
pivot_wider(names_from = names, values_from = value) %>%
CCF(python, r, lag_max = 300) %>%
autoplot()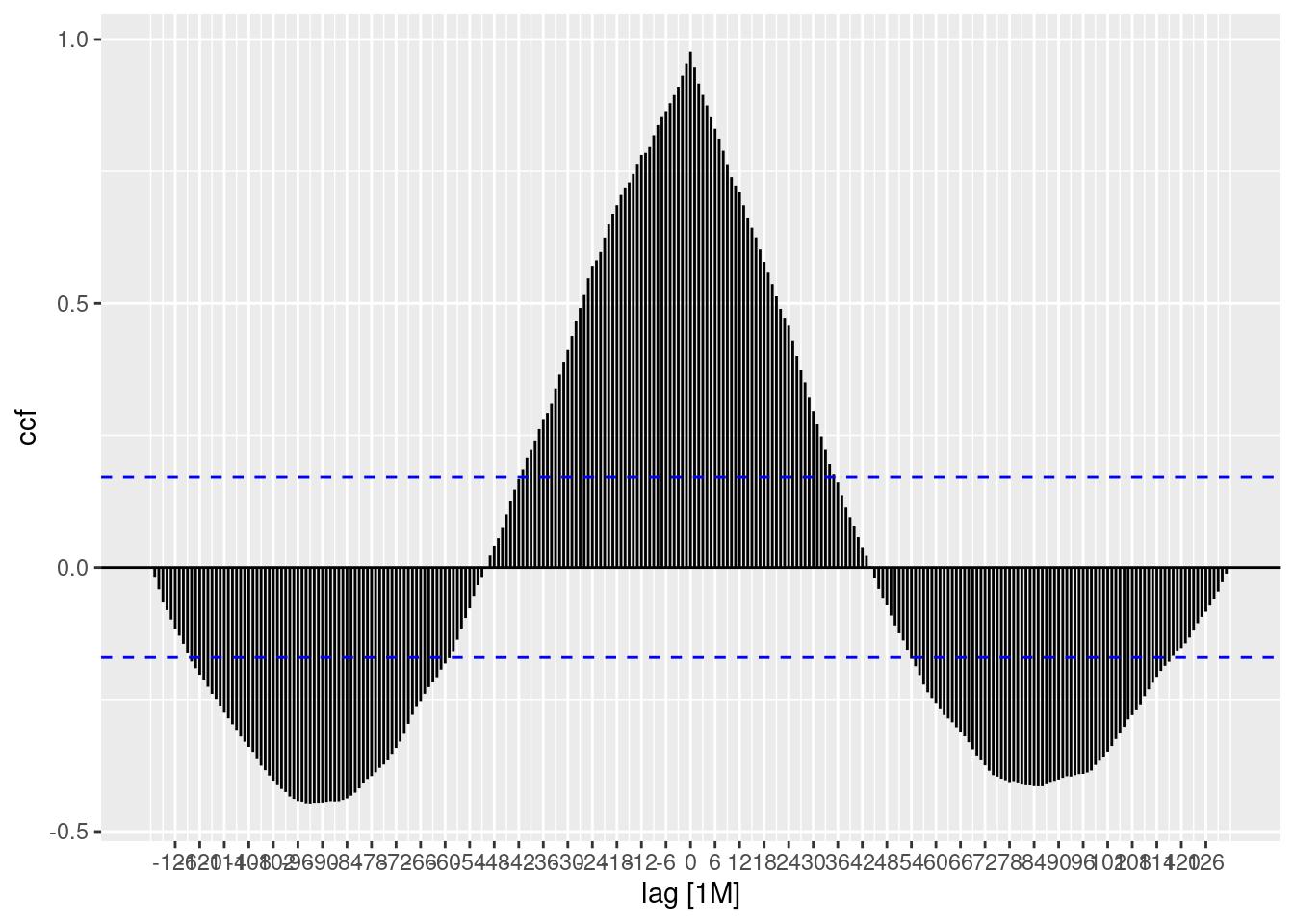
Terceira abordagem (abordagem tidy)
Até agora, mudamos nosso objeto original várias vezes, mas usando o pacote timetk você pode realizar todas essas análises usando apenas o objeto original (tibble). Tornando a análise muito mais intuitiva e também integrando-se com todos os pacotes do dirtverse.
Análise de Defasagem III
utiliza-se duas funções para realizar toda a análise de correlação com muito menos código e mais flexibilidade. A única coisa que você precisa fazer é colocar o conjunto de dados em um formato longitudinal (long).
# passing to a long format
stackoverflow_prep_long_tbl <- stackoverflow_prep_tbl %>%
pivot_longer(cols = c(r, python), names_to = "names", values_to = "value")# the series
stackoverflow_prep_long_tbl %>%
plot_time_series(.date_var = date,
.value = value,
.facet_vars = names)# acf/pacf plots
stackoverflow_prep_long_tbl %>%
group_by(names) %>%
plot_acf_diagnostics(.date_var = date,
.value = value,
.show_white_noise_bars = T)Max lag exceeds data available. Using max lag: 131
Max lag exceeds data available. Using max lag: 131Análise de Causalidade III
No mundo real, a série temporal que você deseja comparar provavelmente não estará no mesmo intervalo que aqui, e provavelmente você precisará fazer alguma transformação para colocar no mesmo intervalo e só então calcular o escore CCF (Cross-Correlation-Function).
# CCF plot
stackoverflow_prep_tbl %>%
plot_acf_diagnostics(.date_var = date,
.value = r,
.ccf_vars = python,
.show_ccf_vars_only = T)Max lag exceeds data available. Using max lag: 131Portanto, as principais conclusões deste tutorial são que o pacote timetk é um grande impulso para sua análise exploratória de dados no contexto de séries temporais. As funções são consistentes e temos interatividade em todas as séries.
O timetk também pode fazer outras análises diferentes:
Sazonalidade
Anomalia
Decomposição STL
Gráficos de regressão